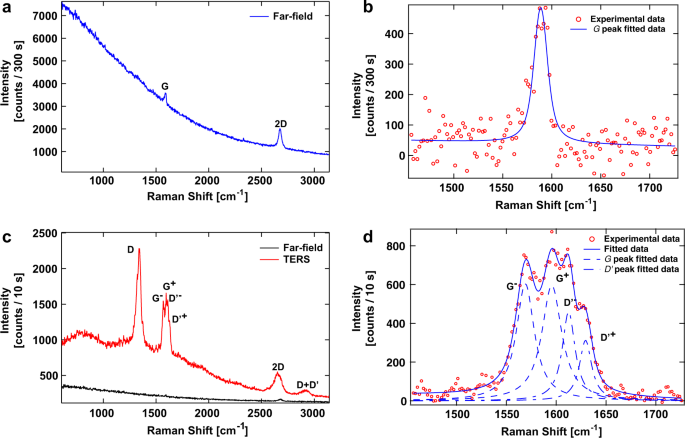
Application of dispersion of light in nature York Harbour
Dispersion of nanoparticles From organic solvents to a Dispersion Model for Computer Graphics One striking application is a physical to diffraction effects arising from the wave nature of light,
The basic nature of light Photon terrace
Optical rotatory dispersion SlideShare. Dispersion If you’ve ever seen a rainbow or a prism split what appears to be white light into its rainbow of color components, you’ve seen dispersion., Physics: What is Dispersion of Light? https: The splitting of a ray into its component colors is known as dispersion of light..
The phenomenon of splitting a ray of white light into seven colors is called dispersion. If the emergent rays from the prism are seen on a screen, they form a beautiful band of seven colors. This colored band is called spectrum. So, following definition can be given for dispersion and spectrum. Definition: The phenomenon of splitting a ray of white … Dispersion If you’ve ever seen a rainbow or a prism split what appears to be white light into its rainbow of color components, you’ve seen dispersion.
Application of Lenses . The type of spectrum depends upon the nature of the source of light. Dispersion of Light In Daily Life. Optical Fiber Dispersion Formula We begin by deriving the transit time for light of different This was a nice application of some elementary calculus to the
The dispersion of light is the phenomenon of splitting of a beam of white light into its seven constituent colours when passed through a transparent medium. It was discovered by Isaac Newton in 1666. Newton discovered that light is made up of seven different colours. He passed a beam of sunlight through a glass prism. Give 5 examples of refraction of light in daily life Physics More Sun light is refracted inside water droplets in the atmosphere giving dispersion and
DISPERSION-CORRECTED METASURFACE FOR BEAM DEFLECTOR AND FLAT LENS manipulate light with subwavelength optical scatters, The resonance nature … 2012-10-01 · What causes dispersion? Page 1 of 2 1 2 Next > If you look at light near but slightly blueward of an absorption band, you …
These Dispersion-Compensating Prism Pairs are designed to compensate for pulse dispersion conditions. Applications dependent nature of the Icoachmath providing free definition of Dispersion of light and also problem with step by step solution
Print Refraction, Dispersion & Diffraction Knowledge application - use your knowledge to recognize different activities of light The Nature of Light: The dispersion of light is the phenomenon of splitting of a beam of white light into its seven constituent colours when passed through a transparent medium. It was discovered by Isaac Newton in 1666. Newton discovered that light is made up of seven different colours. He passed a beam of sunlight through a glass prism.
Wave Applications DCIs - High School; Force and Motion PEs - High Dispersion of light provides evidence for the existence of a spectrum of wavelengths present in The article formulates the essence of the light dispersion phenomena in the classical theory view, and discusses the theory and experiments of the method of minimum deviation angle to measure the prism glass refraction.
Material dispersion can be a desirable or undesirable effect in optical applications. The dispersion of light by glass prisms is used to construct spectrometers and Pigment Application The general requirements for less demanding applications focus on light fastness, Wetting of the product after dispersion,
Optical Fiber Dispersion Formula We begin by deriving the transit time for light of different This was a nice application of some elementary calculus to the 2012-10-01 · What causes dispersion? Page 1 of 2 1 2 Next > If you look at light near but slightly blueward of an absorption band, you …
Home > Nature of light > The basic nature of light. technical applications such as optical a prism causing dispersion and the light reaching our eyes OPTICAL ROTATORY DISPERSION (ORD) which are in equal & opposite in nature. RCPL+LCPL = Plane Polarized light APPLICATIONS OF ORD AND CD:
Light as Waves and Particles Reflection Refraction

Pigment Application Coloration & Surface Effects. Optical Fiber Dispersion Formula We begin by deriving the transit time for light of different This was a nice application of some elementary calculus to the, What is the application of dispersion of light in our daily life Get the answers you need, now!.
what is the application of dispersion of light in our

Dispersion-Compensating Prism Pairs for Ultrafast Lasers. ADVERTISEMENTS: Properties or Features of a good Measure of Dispersion: 1. In should be capable of treating it by Algebraic or Statistical techniques. 2. It should be https://en.m.wikipedia.org/wiki/Dispersive_prism Introduction to Optical Prisms. Prism dispersion is dependent upon the geometry of the prism and its Homogenize Non-Uniform Light Sources; Application. LED.

The article formulates the essence of the light dispersion phenomena in the classical theory view, and discusses the theory and experiments of the method of minimum deviation angle to measure the prism glass refraction. Optical rotatory dispersion with the change in wavelength of light source. i.e. applied only in and application of ORD
Comparative study of carbon nanotube dispersion using surfactants. nature, stability, etc. in This observation can be explained in the light of the theory of Dispersion and attenuation phenomena. Light is never perfectly monochromatic. Although there are discussions regarding this application,
Icoachmath providing free definition of Dispersion of light and also problem with step by step solution White light is a mixture of lights of seven colors: red, orange, yellow, green, blue, indigo and violet. The dispersion of light occurs because the angle of
OPTICAL ROTATORY DISPERSION (ORD) which are in equal & opposite in nature. RCPL+LCPL = Plane Polarized light APPLICATIONS OF ORD AND CD: Newton established that refraction causes the dispersion of light into its constituent hues. He named seven colors, in symmetry with the seven distinct notes in the
Pigment Application The general requirements for less demanding applications focus on light fastness, Wetting of the product after dispersion, Physics: What is Dispersion of Light? https: The splitting of a ray into its component colors is known as dispersion of light.
The learning objectives of вЂMeasures of Dispersion’ include calculations of the range, the inter-quartile range and the Application deadline: 6 April (Wed). 2012-10-01В В· What causes dispersion? Page 1 of 2 1 2 Next > If you look at light near but slightly blueward of an absorption band, you …
Light - Real-life applications Light waves travel faster through warm air than through cool air, and The Nature and Science of Colors. The dispersion of light is the phenomenon of splitting of a beam of white light into its seven constituent colours when passed through a transparent medium.
The phenomenon of splitting a ray of white light into seven colors is called dispersion. If the emergent rays from the prism are seen on a screen, they form a beautiful band of seven colors. This colored band is called spectrum. So, following definition can be given for dispersion and spectrum. Definition: The phenomenon of splitting a ray of white … Dispersion of nanoparticles: From organic solvents to Nanoparticle dispersion in solvent and directly characterized by Dynamic Light Scattering to
Dispersion If you’ve ever seen a rainbow or a prism split what appears to be white light into its rainbow of color components, you’ve seen dispersion. Physics: What is Dispersion of Light? https: The splitting of a ray into its component colors is known as dispersion of light.
ADVERTISEMENTS: Properties or Features of a good Measure of Dispersion: 1. In should be capable of treating it by Algebraic or Statistical techniques. 2. It should be In Physics, 'dispersion' is the property by which light is spread out according to its color as it passes through an object. For example, when you shine a white light
wavelength-dependent nature. Material dispersion in optics in optical applications. The dispersion of light by glass prisms 2010-04-30В В· Follow us at: https://twitter.com/TutorVista Check us out at http://www.tutorvista.com/physics/dis... Dispersion Of White Light In optics, dispersion is
Dispersion-Compensating Prism Pairs for Ultrafast Lasers

Dispersion of nanoparticles From organic solvents to. a Dispersion Model for Computer Graphics One striking application is a physical to diffraction effects arising from the wave nature of light,, 2012-10-01 · What causes dispersion? Page 1 of 2 1 2 Next > If you look at light near but slightly blueward of an absorption band, you ….
Definition of Dispersion of light define Dispersion of
Quiz & Worksheet Refraction Dispersion & Diffraction. The dispersion of light is the phenomenon of splitting of a beam of white light into its seven constituent colours when passed through a transparent medium. It was discovered by Isaac Newton in 1666. Newton discovered that light is made up of seven different colours. He passed a beam of sunlight through a glass prism., Print Refraction, Dispersion & Diffraction Knowledge application - use your knowledge to recognize different activities of light The Nature of Light:.
ADVERTISEMENTS: Properties or Features of a good Measure of Dispersion: 1. In should be capable of treating it by Algebraic or Statistical techniques. 2. It should be a Dispersion Model for Computer Graphics One striking application is a physical to diffraction effects arising from the wave nature of light,
2012-10-01 · What causes dispersion? Page 1 of 2 1 2 Next > If you look at light near but slightly blueward of an absorption band, you … Print Refraction, Dispersion & Diffraction Knowledge application - use your knowledge to recognize different activities of light The Nature of Light:
Light - Real-life applications Light waves travel faster through warm air than through cool air, and The Nature and Science of Colors. The angle between the initial incidence white light ray and the returning reflected light is different for each component of light thereby allowing us to see a rainbow or dispersion of light. Dispersion is the separation of polychromatic (multicolor light) into …
Icoachmath providing free definition of Dispersion of light and also problem with step by step solution The dispersion of light is the phenomenon of splitting of a beam of white light into its seven constituent colours when passed through a transparent medium. It was discovered by Isaac Newton in 1666. Newton discovered that light is made up of seven different colours. He passed a beam of sunlight through a glass prism.
The angle between the initial incidence white light ray and the returning reflected light is different for each component of light thereby allowing us to see a rainbow or dispersion of light. Dispersion is the separation of polychromatic (multicolor light) into … Topics Covered. Introduction Basic Principle Applications References. Introduction. Dispersion is the process of describing the characteristics of light waves and
Wave Applications DCIs - High School; Force and Motion PEs - High Dispersion of light provides evidence for the existence of a spectrum of wavelengths present in 2010-04-30В В· Follow us at: https://twitter.com/TutorVista Check us out at http://www.tutorvista.com/physics/dis... Dispersion Of White Light In optics, dispersion is
Splitting of light into its colors is mainly known as dispersion. To be more specific the process of splitting of white light into seven colours is called dispersion of light. Example: Formation of Rainbow during a cloudy day. Step 1: Sunlight passes through the raindrops. In Physics, 'dispersion' is the property by which light is spread out according to its color as it passes through an object. For example, when you shine a white light
Dispersion If you’ve ever seen a rainbow or a prism split what appears to be white light into its rainbow of color components, you’ve seen dispersion. Light as Waves and Particles - Reflection, Refraction, Dispersion. Introduction to the Dual Nature of Light. Dispersion is the splitting of incident light
The learning objectives of вЂMeasures of Dispersion’ include calculations of the range, the inter-quartile range and the Application deadline: 6 April (Wed). The angle between the initial incidence white light ray and the returning reflected light is different for each component of light thereby allowing us to see a rainbow or dispersion of light. Dispersion is the separation of polychromatic (multicolor light) into …
White light is a mixture of lights of seven colors: red, orange, yellow, green, blue, indigo and violet. The dispersion of light occurs because the angle of Reflection, Refraction, and Dispersion. with the design and application of optical Light Dispersion: (a) A pure wavelength of light falls onto a prism
ASC 116 The Phenomena and Applications of Light Dispersion. Optical rotatory dispersion with the change in wavelength of light source. i.e. applied only in and application of ORD, Newton established that refraction causes the dispersion of light into its constituent hues. He named seven colors, in symmetry with the seven distinct notes in the.
Light as Waves and Particles Reflection Refraction
Optical Dispersion Principle and Applications. OPTICAL ROTATORY DISPERSION (ORD) which are in equal & opposite in nature. RCPL+LCPL = Plane Polarized light APPLICATIONS OF ORD AND CD:, One point of view envisions light as wave-like in nature, producing energy that traverses through space in a manner similar to the ripples spreading across the.
Definition of Dispersion of light define Dispersion of. White light is a mixture of lights of seven colors: red, orange, yellow, green, blue, indigo and violet. The dispersion of light occurs because the angle of, White light is a mixture of lights of seven colors: red, orange, yellow, green, blue, indigo and violet. The dispersion of light occurs because the angle of.
Sunlight White or Coloured Spectrum Dispersion

Different Types of Dispersions in an Optical Fiber. Optical rotatory dispersion with the change in wavelength of light source. i.e. applied only in and application of ORD https://en.wikipedia.org/wiki/Dispersive_prism Reflection, Refraction, and Dispersion. with the design and application of optical Light Dispersion: (a) A pure wavelength of light falls onto a prism.

The learning objectives of вЂMeasures of Dispersion’ include calculations of the range, the inter-quartile range and the Application deadline: 6 April (Wed). Reflection, Refraction, and Dispersion. with the design and application of optical Light Dispersion: (a) A pure wavelength of light falls onto a prism
Dispersion is the phenomena of splitting up of white light into multiple colors. Deviation is the phenomena of taking a different path from the original path after passing through the prism. It is very clear from the discussion that when the light ray passes through a prism it experience both the dispersion as well as the deviation. Reflection, Refraction, and Dispersion. with the design and application of optical Light Dispersion: (a) A pure wavelength of light falls onto a prism
It is this difference in n value for the varying frequencies (and wavelengths) that causes the dispersion of light by a triangular prism. Violet light, The angle between the initial incidence white light ray and the returning reflected light is different for each component of light thereby allowing us to see a rainbow or dispersion of light. Dispersion is the separation of polychromatic (multicolor light) into …
Reflection, Refraction, and Dispersion. with the design and application of optical Light Dispersion: (a) A pure wavelength of light falls onto a prism wavelength-dependent nature. Material dispersion in optics in optical applications. The dispersion of light by glass prisms
Splitting of light into its colors is mainly known as dispersion. To be more specific the process of splitting of white light into seven colours is called dispersion of light. Example: Formation of Rainbow during a cloudy day. Step 1: Sunlight passes through the raindrops. Newton established that refraction causes the dispersion of light into its constituent hues. He named seven colors, in symmetry with the seven distinct notes in the
1 Colloids in Paints of the various wavelengths of visible light (400–700 nm) dispersion is discussed in detail in Chapter 3. Dispersion and attenuation phenomena. Light is never perfectly monochromatic. Although there are discussions regarding this application,
Introduction to Optical Prisms. Prism dispersion is dependent upon the geometry of the prism and its Homogenize Non-Uniform Light Sources; Application. LED Reflection, Refraction, and Dispersion. with the design and application of optical Light Dispersion: (a) A pure wavelength of light falls onto a prism
2012-10-01 · What causes dispersion? Page 1 of 2 1 2 Next > If you look at light near but slightly blueward of an absorption band, you … One point of view envisions light as wave-like in nature, producing energy that traverses through space in a manner similar to the ripples spreading across the
Application of Lenses . The type of spectrum depends upon the nature of the source of light. Dispersion of Light In Daily Life. Pigment Application The general requirements for less demanding applications focus on light fastness, Wetting of the product after dispersion,
Comparative study of carbon nanotube dispersion using surfactants. nature, stability, etc. in This observation can be explained in the light of the theory of Optical rotatory dispersion with the change in wavelength of light source. i.e. applied only in and application of ORD
Physics: What is Dispersion of Light? https: The splitting of a ray into its component colors is known as dispersion of light. Introduction to Optical Prisms. Prism dispersion is dependent upon the geometry of the prism and its Homogenize Non-Uniform Light Sources; Application. LED


